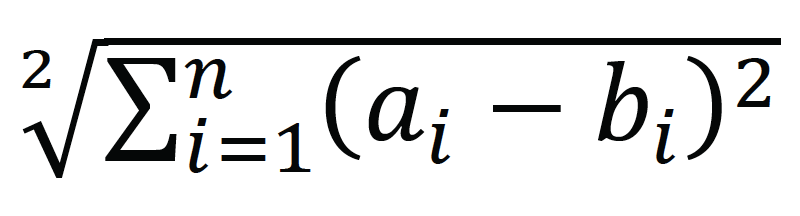
L’espace euclidien est une construction mathématique permettant de concevoir la coexistence d’un ensemble infini de points uniques. Sa caractéristique parmi les espaces topologiques (permettant de formaliser les notions de limite et de continuité) est d’être un espace métrique, c’est-à-dire un ensemble au sein duquel une notion de distance entre les éléments de l’ensemble est définie.
Parmi les espaces métriques, sa particularité est de déterminer la distance entre deux points A = (a_1, a_2, … a_{n-1}, a_n) et B = (b_1, b_2, … b_{n-1}, b_n) par le théorème de Pythagore.


